Matematyka dla każdego

Zad.1

Cena pewnego towaru jest równa 200 zł. Ile wyniesie ta cena po obniżce o 15%?

Zad. 2

Pokój dziecięcy ma 15 m2, co stanowi 25% powierzchni całego mieszkania. Ile wynosi powierzchnia tego mieszkania?

Zad. 3

 W klasie liczącej 36 osób jest 4 nieobecnych. Jaki to procent całej klasy?

Zad. 4

Pewien towar kosztował x zł. Jego cenę najpierw podwyższono o 20%, następnie obniżono o 15%. Ile teraz kosztuje ten towar?

Zad. 5

Jakim procentem wszystkich liter w wyrazie MATEMATYKA są samogłoski?

Zad. 6

Proszek „Błysk” podrożał o 5% i kosztuje teraz 6,30 zł. Ile kosztował przed podwyżką?

Zad.7

Bok pewnego kwadratu zwiększono o 7%. Jak zmieniło się jego pole?

Fajnie mieć swojego bliźniaka, nie? Moglibyśmy wszystko mieć podobne: dzielić się ubraniami, wyglądać tak samo... kto wie, może i nauczyciele by się nie połapali???? :)

Kolejnymi ciekawymi liczbami w matematyce są właśnie liczby bliźniacze. 

Są to dwie liczby pierwsze (czyli podzielne przez 1 i siebie samą -przyp. red.), które różnią sie o 2.

Łatwo nam będzie odszukać takie liczby, bo jest ich naprawdę dużo :  3 i 5, 5 i 7, 11 i 13, 17 i 19, 21 i 23 ....

Do dnia dzisiejszego nie wiadomo czy istnieje nieskończenie wiele par bliźniaczych! 

Zad. 1

Jeden z kątów przyległych ma miarę 38 stopni. Oblicz miarę drugiego kąta.

Narysuj te kąty za pomocą kątomierza.

Zad. 2

Jeden z kątów wierzchołkowych ma miarę 27 stopni. Oblicz pozostałe kąty.

Zad. 3

Jeden z kątów przyległych jest o 43 stopnie większy od drugiego. Oblicz miary tych kątów. Zapisz obliczenia.

Zad. 4

Czy suma dwóch kątów ostrych jest zawsze kątem rozwartym? Odpowiedź uzasadnij.

Zad. 5

Miara jednego z kątów przyległych jest 11 razy większa od miary drugiego kąta. Ile wynosi różnica miar tych kątów?

W matematyce jest wiele ciekawych liczb.  Na początek poznajmy liczby doskonałe. I wcale nie chodzi o to, że są piękne, kształtne czy nadzwyczaj często używane :)

Liczba doskonała ma pewną ciekawą własność i zacznijmy od tego, że musi być liczbą naturalną. Jest ona jednocześnie równa sumie wszystkich swoich dzielników,

mniejszych od siebie samej.

Liiczba 6 jest liczbą doskonałą. Czemu? Wiemy, że jej dzielnikami są po kolei 1, 2, 3 i 6. Skoro mamy zsumować wszystkie jej dzielniki, które są mniejsze od niej samej to

po dodaniu :  1 + 2 + 3 otrzymamy właśnie 6.

Liczba 28 także jest liczbą doskonałą. Jej dzielniki to 1, 2, 4, 7, 14 i 28. Po dodaniu wszystkich dzielników mniejszych od 28 otrzymam....

1 + 2 + 4 +7 + 14 = 28 

Kolejną liczbą jest 496.  Przez jakie liczby się dzieli? 1, 2, 4, 8, 16, 31, 62, 124, 248 i 496. I znowu dodajemy wszystkie dzielniki mniejsze od 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248  = 496   :)

To były trzy najmniejsze liczby doskonałe.

8128

Oblicz, pamiętając o kolejności wykonywania działań ( jeden podpunkt to jedno zadanie):

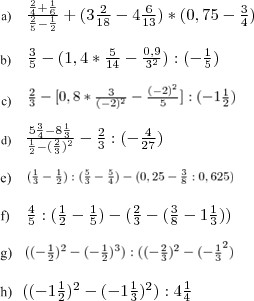
Zad. 1 

Zamień procenty na liczby:

35%, 64%, 134%, 365%, 0,34%, 12% 34,8%, 90754%, 476443546%

Zad.2

Zamień liczby na procenty:

2 ; 65 ;  0,43 ;  1,46 ; 34,76 ; 5 ; 128

Zad.3

Ile wynosi:

a). 2% liczby 30

b). 26% liczby 130

c). 5% liczby 5

d) 0,45% liczby 12

Zad.4

Wyznacz liczbę o :

a). 2% mniejszą od 16

b) 10% większą od 100

c) 30% większa od 1200

d) 22% mniejszą od 4580

Zad. 1

Narysuj trapez równoramienny o podstawie dolnej równej 6 cm, podstawie górnej 4 cm i wysokości równej 3 cm.

Zad.2

Narysuj trapez prostokątny o wysokości 5 cm, podstawie dolnej 4 cm i górnej 2 cm.

Zad.3

Kąt ostry trapezu równoramiennego wynosi 28 stopni. Oblicz pozostałe kąty tego trapezu.

Zad. 4

Kąt rozwarty trapezu prostokątnego ma miarę 131 stopni. Oblicz pozostałe kąty tego trapezu.

Zad.5

Odpowiedz tak lub nie i uzasadnij:

a) Kwadrat jest trapezem

b) Prostokąt jest rónoległobokiem

c). Każdy trapez jest równoległobokiem

d) Każdy równoległobok jest rombem

Zad.6

Jeżeli jeden z kątów rombu ma miarę 35 stopni, to czy jeden z pozostałych kątów może mieć 125 stopni?

Zad. 7

W trapezie równoramiennym podstawa dolna ma 12 cm, podstawa górna jest dwa razy krótsza od podstawy dolnej, a ramię trapezu jest o 2 cm krótsze od podstawy górnej. Oblicz obwód tego trapezu równoramiennego.

Rok 2020 będzie szczególny. Wiadomo-każdego z nas czeka szczęście, zdrowie, miłość, spełnianie marzeń  :) ... ale rok 2020 to też ciekawa matematyczna liczba. Tzw. liczba autobiograficzna. Niewiele liczb ma taką własność jak ta data, bo zaledwie siedem ! Co właściwie oznacza liczba autobiograficzna?

2 0 2 0

Pierwsza cyfra  ( w tym przypadku 2 ) mówi o ilości zer w całej liczbie (zgadza się? No tak, bo mamy dwa zera)

Druga cyfra ( w tym przypadku 0 ) mówi o ilości jedynek w całej liczbie (rzeczywiście nie mamy żadnych jedynek w naszej liczbie)

Trzecia cyfra ( w tym przypadku znowu 2 ) mówi o ilości dwójek w całej liczbie ( i mamy je dwie )

Czwarta cyfra ( w tym przypadku znowu 0 ) mówi o ilości trójek w całej liczbie ( i znowu mamy ich brak, więc wszystko się zgadza ).

Inne liczby autobiograficzne to : 1210, 21200, 3211000, 42101000, 521001000, 6210001000.

Zadania dodatkowe z równoległoboków:

1. Narysuj dwa różne równoległoboki, których obwód wynosi  36 cm.

2. Oblicz i wpisz brakujące miary kątów równoległoboków :

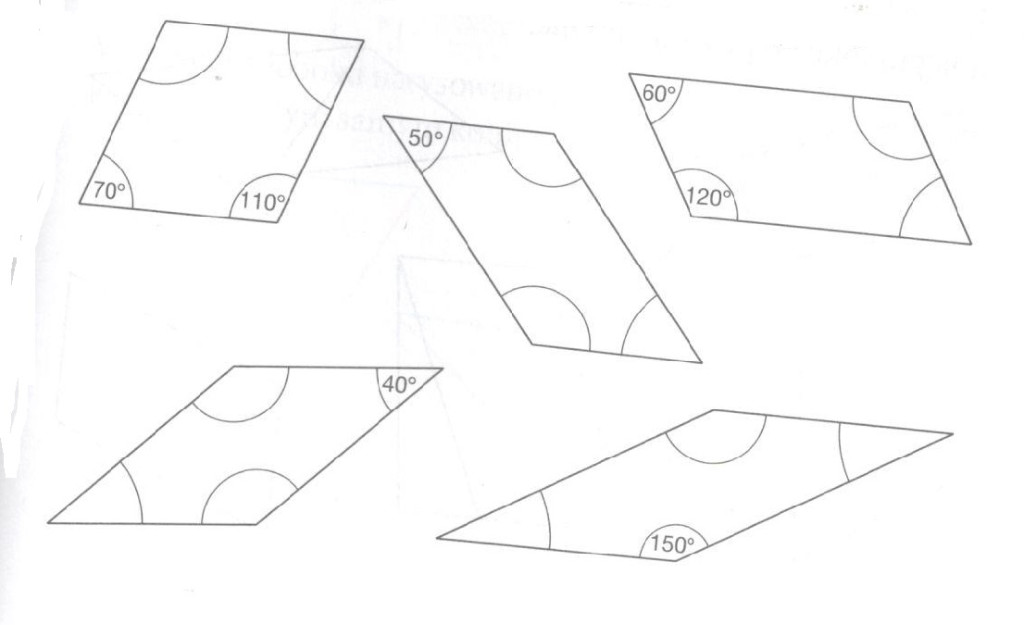
3. Narysuj romb o przekątnych 6 cm i 4 cm. Narysuj za pomocą ekierki jego wysokość i zmierz ją.

4. Oblicz:

a). jeden z boków równoległoboku, którego obwód wynosi 92 cm, a drugi bok ma 16 cm długości.

b). bok rombu, którego obwód wynosi 52 dm.

Cześć ! Nazywam się Paulina i uczę matematyki w szkole podstawowej.

Witam wszystkich moich uczniów z SP134 i innych, którzy tu zabłądzili :)

Blog ma służyć do ułatwiania nam kontaktu, zamieszczania materiałów i zadań pomagających w prowadzeniu lekcji, jak i w Waszej samodzielnej pracy. Enjoy !